Previous ThursdayThoughts presented the concept that Somethings were behaving as though they were chaotically moving in Nothing. Order from chaos started when two Somethings chanced to contact each other.

Precisely how Order began by the chance contact of two Somethings must be considered speculative at this point in the logic. Only when we see where this speculation leads can confidence emerge.

At the moment of contact between two Somethings communication between them of their relative 'motion' becomes possible. Motion requires some concept of extension and of time. Neither of these concepts exists in the void of Nothing.

Understanding how the interaction between Somethings resolves is central to understanding how the Fabric of Space originates. I tried for three years to determine the interaction before abandoning a direct analysis approach. Instead, I resorted to a 'good guess' approach. It was not until twelve years later that results convinced me of the efficacy of the 'good guess'.

The assumptions as to how Somethings interact were quite simple. After all, it seems that Nature would behave in a simple fashion. The primary assumption was that opposing motions would simply cancel each other. It was also assumed that the instantaneous resulting motions of two Somethings would be in the same 'direction' with the same 'velocity'.

There was only one resulting motion that seemed to work with these assumptions. If the resulting motion of each Something canceled all motion except for a circle upon a circle then the primary assumption could be satisfied.

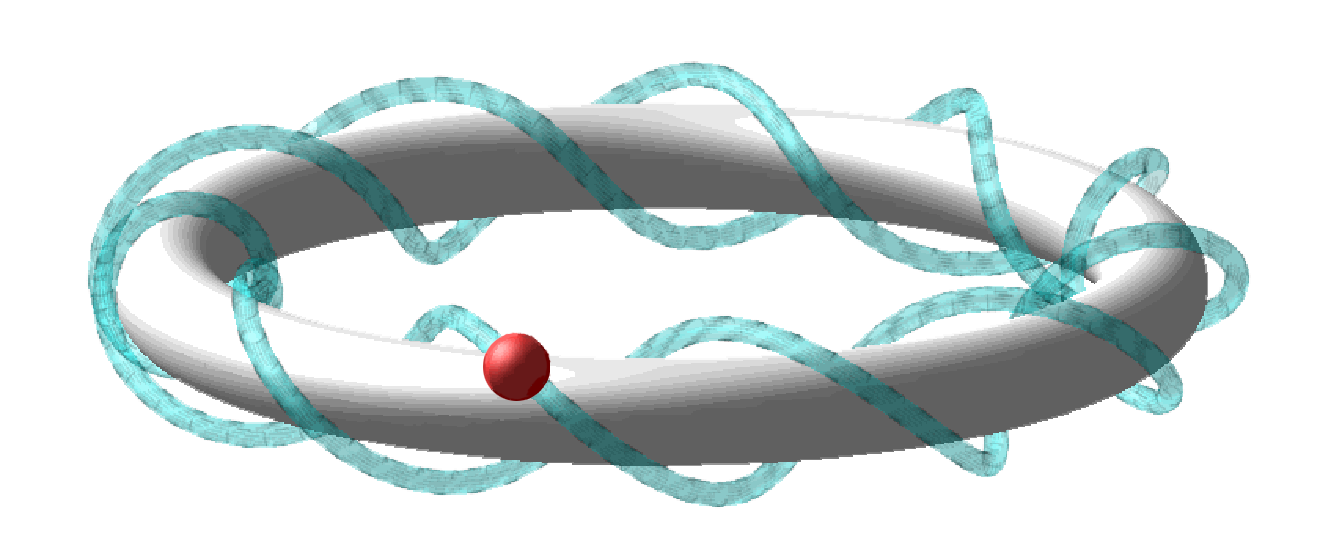
Recall in the Chaos thought that chaotic motion could be considered as resulting from circular motion upon circular motion. A visual analogy of the resulting motion is that of a torus or donut. Remember that the torus is only a path that Something follows. That path would resemble a Slinky wrapped around on itself. It is helpful to view an analogous image of this(shown above). The red dot illustrates 'Something'. The remainder of the image illustrates the path. This illustration is only a physical representation of a metaphysical reality.

Until only two years ago I wondered how the Something could follow the donut path and later contact the other Something again. The answer was surprisingly simple.

In the shared coordinate system formed by the contact of the two Somethings, the resulting motion could be considered as being tangential. In other words, in that shared coordinate system the Somethings were sure to return to the point of contact for an indefinite number of times. They needed only to eventually return at the same moment.